Десятки
Когда речь идёт о больших числах, то счёт удобно вести десятками или даже сотнями, тысячами и т.д.
Если взять один десяток каких-то предметов, то говорят,
что взяли десять: 10,
если два десятка – двадцать: 20,
три десятка – тридцать: 30,

четыре десятка – сорок: 40,
пять десятков – пятьдесят: 50,
шесть десятков – шестьдесят: 60,
семь десятков – семьдесят: 70,
восемь десятков – восемьдесят: 80,
девять десятков – девяносто: 90,
десять десятков – одна сотня или сто: 100.
Запомните, как называются и записываются эти числа.
Числа, которые оканчиваются одним или несколькими нулями, называются круглыми числами.
Действия с круглыми числами
Круглые числа, в том числе и десятки, складываются, вычитаются и сравниваются так же, как и единицы.
Например: 1). К двум десяткам прибавить четыре десятка, получим 6 десятков. Какому числу соответствуют 6 десятков? Числу 60.
2). Что больше: семь десятков или пять десятков? Семь десятков.
3). Семь десятков вычесть пять десятков, получим 2 десятка. Какому числу соответствуют 2 десятка? Числу 20.
Однозначные и двузначные числа. Цифры
Система счисления, которой мы пользуемся в математике, называется десятеричной, поскольку мы используем в ней для записи чисел десять знаков. Это цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Числа состоят из цифр, как слова из букв.
Рассмотрим для примера ряд чисел: 3; 14; 27; 0; 1; 89. Чем они отличаются?
Для записи чисел 3; 0; 1 используется одна цифра, для записи чисел 14; 27; 89 используются две цифры.
То есть для записи первой группы чисел используется один знак, поэтому такие числа называются однозначными, а для записи второй группы чисел используются два знака, поэтому такие числа называются двузначными. Бывают и трёхзначные, и четырёхзначные, и другие многозначные числа.
Из двух разных цифр, не считая нуля, можно составить два различных числа. Например: 27 и 72.
Одинаковое ли значение в этих числах имеет цифра 2?
В записи числа 27 цифра 2 показывает количество взятых десятков, а в записи числа 72 цифра 2 показывает количество единиц.
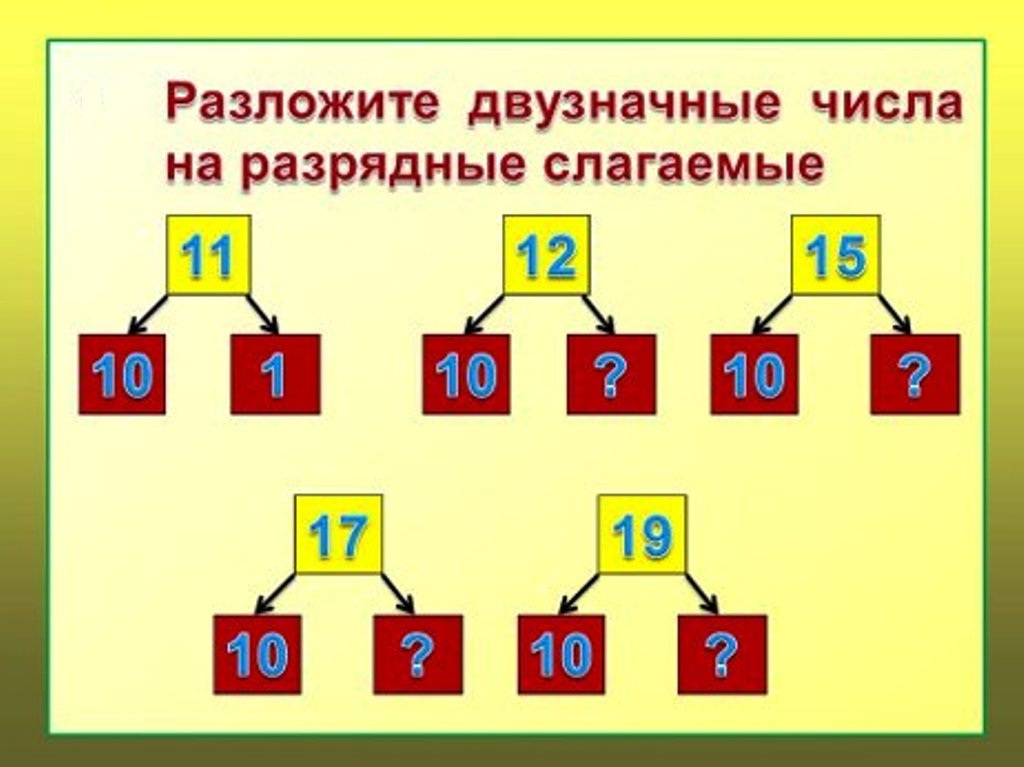
Любое двузначное число можно представить как сумму десятков и единиц: 27 = 20 + 7; 72 = 70 + 2.
А какое значение имеет цифра ноль, например, в числе 40?
Она показывает, что на данной позиции нет значимой цифры. Но это место нельзя оставлять пустым, иначе число станет однозначным. Для того и придумали цифру ноль, чтобы показать, что на месте единиц у числа 40 не взято нисколько единиц.
Так, двузначные числа состоят из десятков и единиц, трёхзначные из сотен, десятков и единиц, и т.д.
А каково самое маленькое и самое большое двузначное число?
Самое маленькое – это число 10. Оно круглое, поскольку на месте единиц у него стоит цифра 0.
Самое большое двузначное число – это число 99. Оно некруглое, так как на месте единиц у него стоит цифра 9.
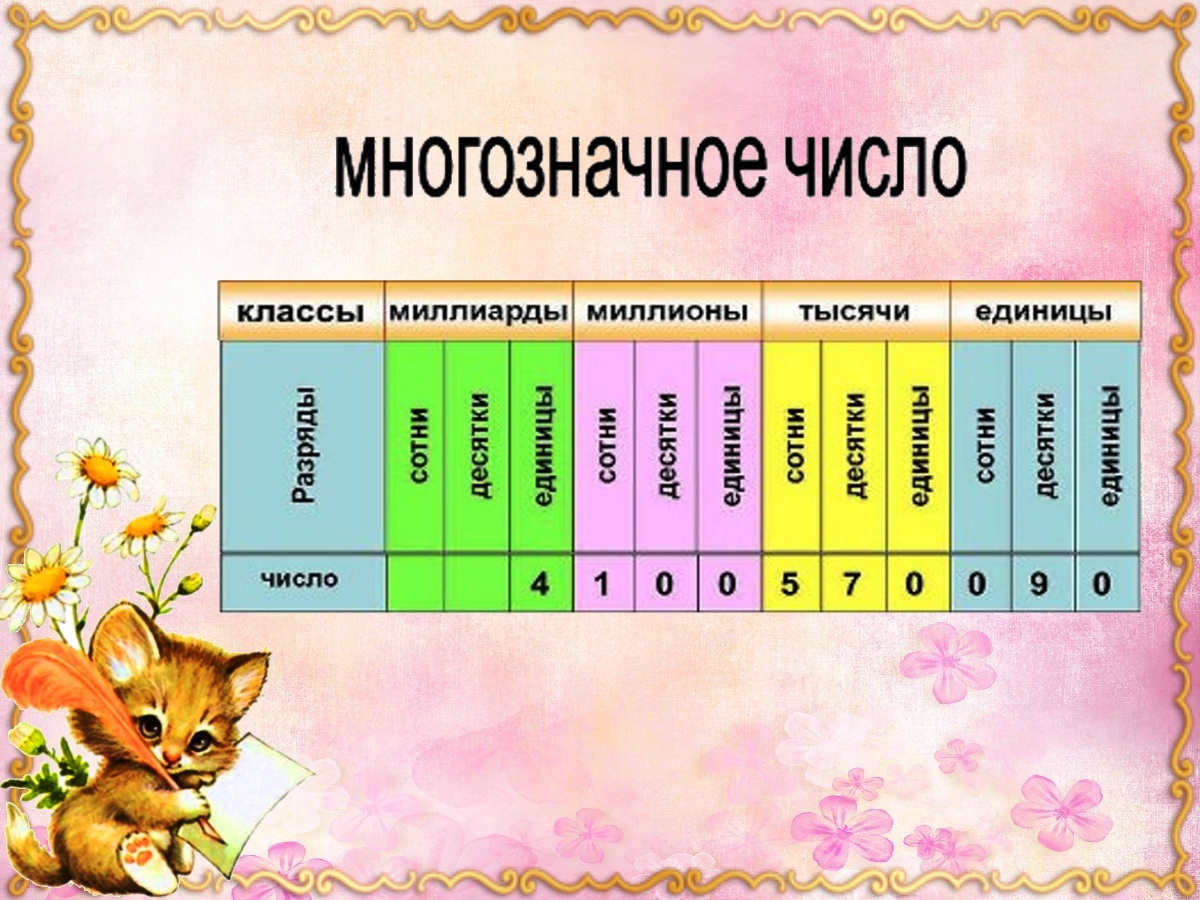
Поскольку значение цифры в числе зависит от её местоположения или позиции, то используемую в математике систему счисления называют также ещё и позиционной. Занимаемую цифрой в конкретном числе позицию называют её разрядом: крайний слева – старший разряд, крайний справа – младший. Например, разряд сотен, разряд десятков и разряд единиц у числа 375 = 300 + 70 + 5.
Запись числа в виде суммы сотен, десятков и единиц называется представлением чисел в виде суммы разрядных слагаемых.
Очень важно уметь определять разрядную цифру, поскольку и сложение, и вычитание, и сравнение чисел происходит поразрядно.
Сравнение двузначных чисел
Сравним двузначные числа 27, 23 и 35. Сравнивать начнём с наивысшего разряда – с разряда десятков.
27 = 20 + 7; 23 = 20 + 3; 35 = 30 + 5.
В числе 35 – три десятка, а в числах 27 и 23 – по два десятка. Значит, наибольшим будет число 35, поскольку 3 > 2, то есть 3 десятка > 2 десятков. Получаем: 35 > 23 и 35 > 27.
В числах 27 и 23 – по два десятка, но в числе 27 больше единиц 7 > 3, значит оно больше: 27 > 23.
Ответ: из чисел 27, 23 и 35 наибольшее – 35, наименьшее – 23.
Правило сравнения чисел:
- Больше то число, которое содержит большее число разрядов.
- При одинаковом количестве разрядов сравнивать необходимо начинать с наивысшего разряда. Больше то число, у которого больше цифра в наивысшем разряде.
- Если в наивысшем разряде количество единиц совпадает, то следует переходить к следующему за ним разряду и сравнивать количество единиц в следующем разряде.
Числовой ряд, используемый при счёте предметов, не ограничивается ни сотнями, ни тысячами, поскольку для каждого числа из этого ряда есть последующее число, то есть число, большее на единицу.
А для всех ли чисел в нём есть предыдущие число, то есть число, меньшее на единицу. Нет, для единицы нет предыдущего, поскольку ноль, меньший на один, чем единица при счёте не используется.